工事担任者　取得の道しるべ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ※非定期に加筆更新しています。　 　　　　　 　　　　　念のため，　　再読み込みをしてみてください！
	『　電気気通信技術の基礎　』
	問題１の（2）交流回路	初版　2017/01/02 改版　2020/12/10
	平成２３年第２回　〜　Ｈ２８年第２回までの１１回の既出問題を整理して並べてみました 　　　基本的な原理・原則の応用により， 　　　　　　簡易な計算で，短時間で確実に答えることができます。 　既出問題の分析 　　毎回，　『直列接続』か『並列接続』から１問が出題（5点）されています。　 　　こつを掴めば，確実に得点できる貴重なサービス問題です。 　　目標回答時間：４分弱（解き方の見通し〜算出〜検算〜回答用紙への記入まで） 　　具体的な必要スキル 　　　　ＬＣＲ　【直列】 接続では，【電圧のベクトル図】 　　　　ＬＣＲ　【並列】 接続では，【電流ベクトル図】　　　　を自在に描ける力 　　　　　　　　　　　そもそも，なぜ直列では電圧ベクトル 　　　　　　　　　　　並列接続では電流ベクトルを用いるのか・・・理解していますか？ 　　　　　　　　　　　 　　　　簡単な三角関数の計算能力　 　　　　　　（例）　直角三角形の　各辺の比率の代表例　３：４：５・・・・頻出⇒時短回答力が有効に使えます 　　　　　　　　　　　　　直角三角形の2辺に，３，４，５の内の二つの数値が出てきたら， 　　　　　　　　　　　　　残りの１辺は，残った数値になるというものです。 　　　　　　　　　　　　　これを自由に扱えると，驚くほど速く回答にたどり着けます。 　　　　　　　　　　斜辺の長さの求め方（ピタゴラスの定理）　・・・・・・・必須 　　　　平方根の算出能力 　　　　　　　√６２５＝？　　逆算法（回答例を二乗し６２５になるものを探す）で回答見つけれます。 　　　　　　　　　　　　　　　　　もちろん，正攻法で 　　　　　　　　　　　　　　　　　６２５を割り算できそうな数で次々に割っていく方法もありますが，焦っていると 　　　　　　　　　　　　　　　　　３０秒弱でできるこの計算も，数分経っても解けないこともありえます！　 　　　　　　　　　　　　　　　　　そこで，荒っぽい検算力 　　　　　　　　　　　　　　　　　　　２０の二乗は４００ 　　　　　　　　　　　　　　　　　　　３０の二乗は９００ 　　　　　　　　　　　　　　　　　　　　　６２５の平方根は２０と３０の間になりそうと判りますね。 　　　　　　　　　　　　　　　　　　　　　　答えの選択肢の中に’２５’を見つけ一桁目の二乗が２５・・・もう決まりですね。 　　　　※回答法の理解を進める時期では 　　　　　　　　　　　正攻法で勉強を進めてください。 　　　　※回答法の道筋が理解できたら 　　　　　　　　　　　４分以下で解けるようテクニックを磨いてください。 　　　　　　　　　　　慣れてくると，設問自体が時短回答テクニックが活用できる，作りになっていることに気づく 　　　　　　　　　　　と思います。 　 　　　　　　　　　　　話はそれますが 　　　　　　　　　　　電気設備や回路設計の分野では，仔細な計算は自動化（換算表含む）されている場合が多く， 　　　　　　　　　　　細かな計算を筆算で行うことは稀です。 　　　　　　　　　　　技術者は，基本原理に基づいた荒っぽい計算で大まかな値をつかみ，目の前の事象に適格に 　　　　　　　　　　　対応する役割が求められます。　 【問題１】　（２）交流回路 配点 R02 H31 H30 H29 H28 H27 H26 H25 H24 H23 #2 #1 #2 #1 #2 #1 #2 #1 #2 #1 #2 #1 #2 #1 #2 #1 #2 #1 #2 #1 直列接続 ａ．Ｒ Ｌ 3回 ５点 中止 (ａ') (a) (a') ｂ．ＲＬＣ 5回 (b''') (b'') （ｂ） (b') (b'') ｃ．ＲＬＣ 2回 (c') (c) 並列接続 ｄ．ＬＣ 5回 (d'') 中止 (d''') (d) (d'') (d') ｅ．ＲＬＣ 1回 (e) ｆ．ＲＬＣ 2回 (f) (f) 『直列接続』か『並列接続』のどちらかが出題される。 いづれの問題も，基本を押さえていれば確実に答えれる【サービス問題】です。　　凡ミスしないよう回答力を高めましょう！
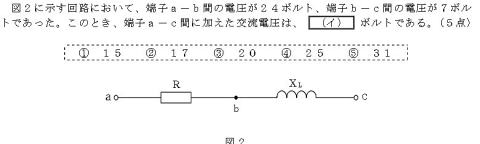
(a)	2016（H28)#2_問題２_（２）	求められるスキル 　　電圧のベクトル図（直角三角形）を描けること 　　直角三角形の斜辺の長さを求める力 　　　　求める電圧　＝√（24×24＋７×７） 　　　　　　　　　　　　＝√（576＋49） 　　　　　　　　　　　　＝√625 　　　６２５÷５÷５÷５÷５＝１　　 　　　　　から 　　　２５にたどり着くのが正攻法ですが 　　　この先は，�@〜�Dの値を二乗して， 　　　６２５になるものを探しても良い 　　　　　�B２０⇒400　なのでちがう 　　　　　�C２５⇒一桁目の５の二乗は２５ 　　　　　�D３１⇒３０の二乗は９００・・大きすぎ　 　　　　　　という算段して，答え�Cにたどり着く。 全く解き方が全く思い出せなかった時は、 　　抵抗＋抵抗ではないから　２４＋７＝３１でない 　　Ｌ＋Ｃ　ではないから　２４−７＝１７でもない 　　　　その間の�B�Cがあやしいい 　　　　また直流抵抗の電位差より端子ａ−ｃが低く 　　　　ないと判断できれば・・・・絞りこめる。
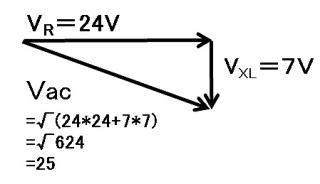
（a'）	2013（H25)#2_問題2_(2)	2013(H25)#2 H28#2と各素子の値が異なるだけ step1：電圧のベクトル図をイメージ step2：求める値は，ベクトル図の斜辺と気づく。 step3：ピタゴラスの定理を思い出す 　　　　　　求める電圧＝√（１５×１５＋８×８） 　　　　　　　　　　　　　＝√（225＋64） 　　　　　　　　　　　　　＝√（289） 　　�A10　の二乗は100・・・小さい 　　�C19　２０の二乗は400・・大きすぎる 　　�B17　一桁目の７の二乗・・・４９・ 　　　　　　　　　　　　　　　　　　・一桁目一致 　　　　　　　　　　　　17＊17＝289・・・ヒット 　　そもそも、 　　二辺の長さが１５，８の斜線部の長さは， 　　目測でも15より少し大きな値になりそうなこと 　　わかる。　また�C１９の二乗は400に近いし・・・。
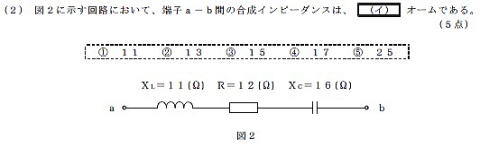
(b)	2016(H28)#1_問題2_(2) 　　　　端子ａ−ｂ間の合成抵抗を求めよ（�@〜�Dから選択）	2016(H28)#1　合成抵抗を求める 求められるスキル 　　電圧のベクトル図（直角三角形）を描けること 　　 直角三角形の斜辺の長さを求める力　　 step1：インピーダンスのベクトル図をイメージ step2：べクトル図（頭の中）でＸＬとＸＣの差分を用 　　　　　いること思い出す step3：求める値が斜辺だと気づく 　　　　 求める値＝√（１２２＋（ＸＣ−ＸＬ）２） 　　　　　　　　　　　 　＝√（144＋52） 　　　　　　　　　　　　 ＝√（169） 　　　　　もともと，二辺が１２と５なので斜辺は１２より 　　　　　わずかに大きいときづけば・・・�Aがあやしい 　　　　　�@〜�Dの一桁目の数値を二乗して９になる 　　　　　のは 　　　　　�A・・・・ヒット
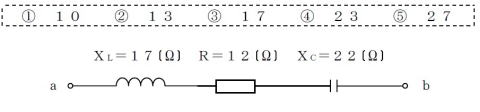
(b')	Ｈ２６＃１　端子ａ−ｂ間の合成抵抗値を求めよ	H26#1　合成抵抗の算出 求められるスキル 　　電圧のベクトル図（直角三角形）を描けること 　　 直角三角形の斜辺の長さを求める力　　 step1：インピーダンスのベクトル図をイメージ step2：べクトル図（頭の中）でＸＬとＸＣの差分を用 　　　　　いること思い出す step3：求める値が斜辺だと気づく 　　　　 求める値＝√（１２２＋（ＸＣ−ＸＬ）２） 　　　　　　　　　　　 　＝√（144＋52） 　　　　　　　　　　　　 ＝√（169） 　もともと，二辺が１２と５なので斜辺は１２より 　わずかに大きいときづけば・・・�Aがあやしい 　�@〜�Dの一桁目の数値を二乗して９になるのは 　�A・・・・ヒット
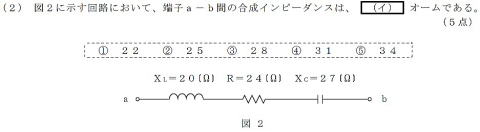
(b'')	Ｈ２３＃２　端子ａ−ｂ間の合成抵抗値を求めよ	H23#2 　合成抵抗の算出　 求められるスキル 　　電圧のベクトル図（直角三角形）を描けること 　　 直角三角形の斜辺の長さを求める力　　 step1：インピーダンスのベクトル図をイメージ step2：べクトル図（頭の中）でＸＬとＸＣの差分を用いること 　　　　思い出す step3：求める値が斜辺だと気づく 　　　　　　 求める値＝√（24２＋（ＸＣ−ＸＬ）２） 　　　　　　　　　　　 　＝√（576＋72） 　　　　　　　　　　　　 ＝√（625） 　　　　　もともと，二辺が24と7なので斜辺は24より 　　　　　わずかに大きいときづけば・・・�Aがあやしい 　　　�@〜�Dの一桁目の数値を二乗して5になるのは 　　　�A・・・・ヒット　　たしかに25×２５＝625
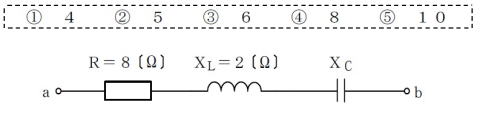
(c)	合成インピーダンスが１０Ωのとき，ＸＣの値は？	Ｈ２６＃２　 　　　 求められるスキル 　　インピーダンスのベクトル図を描けること 　　直角三角形の斜辺が１０，底辺が８のときの 　　高さＸを算出 　　　　　１０　＝√（８×８＋Ｘ２） 　　　　　１００＝（６４ ＋ Ｘ２ ） 　　　　　　Ｘ２＝１００−６４ 　　　　　　Ｘ　＝√３６ 　　　　　　　　＝６ 　　ここでせっかちに答えは�B６　としては残念！ 　　２Ωを引いて６Ωとなる値　�C８Ωが正答
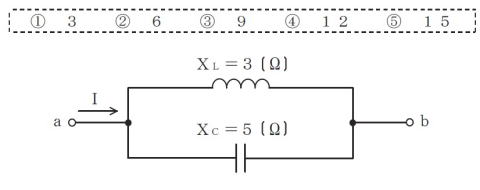
(d)	Ｈ２７＃２ 　　　　端子ａ−ｂに交流４５ｖを加えた際の，全電流Ｉ（Ａ） 　　　（�@〜�Dから選択）	H27#2 step1：並列なので、電流のベクトル図で解くと気づくこと 　　　　　直流抵抗Ｒが含まれないので， 　　　　　ベクトルは，上向きと下向きのみ step2：ＸＬ，ＸＣとも端子電圧は４５Ｖ 　　　　　　各電流は　　 　　　↓45V / ＸＬ Ω＝１５ Ａ 　　　↑45V / ＸＣ Ω＝　９ Ａ step3： 　　　　　　電流ベクトルの向きは上と下向き 　　　　　　求める値は，差分なので 　　　　　　　　答えは　�A６Ａ　です
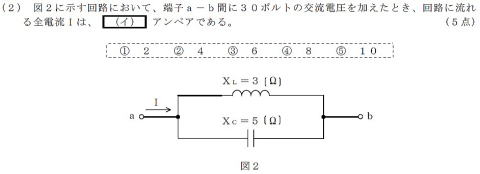
(d')		H24#1 step1：並列なので、電流のベクトル図を使用と気づく step2：ＸＬ，ＸＣとも端子電圧は３０Ｖ 　　　　　　したがって各電流は　　 　　　↓30V / ＸＬ Ω＝１0 Ａ 　　　↑30V / ＸＣ Ω＝　6 Ａ step3： 　　　　　　電流ベクトルの向きは上と下 　　　　　　求める値は，差分なので 　　　　　　　　答えは　�A4Ａ
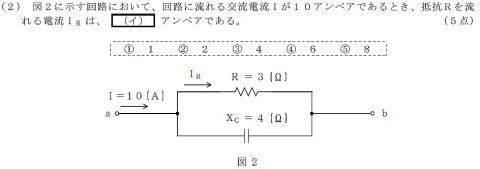
(d'')	Ｈ２４＃２	H24#2 　　【正攻法】 step1：Ｒの端子電圧がわかれば， 　　　　　　　ＩＲが算出できると気づく。 step2：Ｒの端子電圧Ｖabを求めるには， 　　　　　　　ＲとＸＣの合成抵抗値を算出し 　　　　　　　て・・・・ 　　　　　　　　　　　 　　 1/ｚ＝√（（1/R)２＋（1/ＸＣ）２） 　　　　　＝√（1/9＋1/16） 　　　　　＝√（（16+9) / 9*16)） 　　　　　＝√（25 / 9*16） 　　　　　＝√（5×5） / √（3×3×4×4） 　　　　　＝ 5/12 　　　　Ｖab＝ＺＩ＝12/5＊10＝120/5＝24　（Ｖ） 　　　　IR=Ｖab/R＝24/3＝８　（Ａ） 　　【別の解き方】 　　　　　題意から， 　　　　　電流ベクトル図を，絶対値でなく相対値で 　　　　　扱う方法， 　　　　　　　　　底辺（ＩＲ）が1/3 　　　　　　　　　高さ（Ｉc）が1/4 　　　　　　　　　　　これを通分すると 　　　　　　　　　底辺（ＩＲ）が　4/12 　　　　　　　　　高さ（Ｉc）が　3/12 　　　　　　　　　　　相対値だから 　　　　　　　　　底辺（ＩＲ）が　4 　　　　　　　　　高さ（Ｉc）が　3 　　　　　　　　　　　すると斜辺は５ 　　　　　　　　　斜辺が10Aだから 　　　　　　　　　　　ＩＲは４の二倍　　⇒　８Ａ　 　　　　　こちらの方が，計算は早い！ 初出：2017/02/12　 改版：2020/12/11
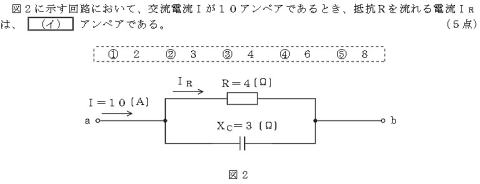
(d''')	（H29）#1_問題1(2) 2020(R02)#2_問題１(2)	H29#1 （ｄ’’）のＲとＸＣの値入れ替えただけの違い 　【正攻法】は（ｄ’’）の解き方参照 　【正攻法でない別の解き方】 　　　　　題意から， 　　　　　電流ベクトル図を，絶対値でなく相対値で 　　　　　扱う方法， 　　　　　　　　　底辺（ＩＲ）が1/4 　　　　　　　　　高さ（Ｉc）が1/3 　　　　　　　　　　　これを通分すると 　　　　　　　　　底辺（ＩＲ）が　3/12 　　　　　　　　　高さ（Ｉc）が　4/12 　　　　　　　　　　　相対値だから 　　　　　　　　　底辺（ＩＲ）が　３ 　　　　　　　　　高さ（Ｉc）が　４ 　　　　　　　　　　　すると斜辺は５ 　　　　　　　　　斜辺が10Aだから 　　　　　　　　　　　ＩＲは３の二倍　　⇒　６Ａ　 　　　　　こちらの方が，計算は早い！
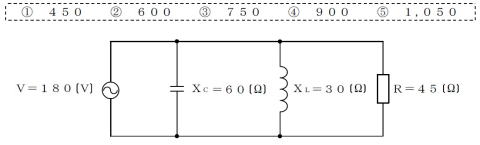
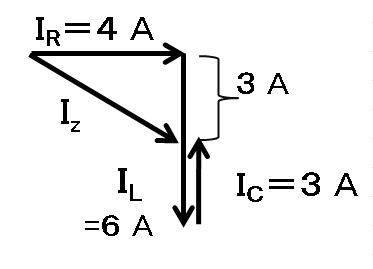
(e)	H27#1_問題2_(2)	H27#1 　【解き方】 　　　各素子の電流を求め，電流ベクトル図で表す 　　　　　　　※アハハ（お詫び）ＩＬとＩＣの向き逆でした！ 　　　　　　　※近日中に直したいと思います・・恥ずかしい。 　　　　　　　※答えの算出には影響しませんが・・・。 　　　　　　　　 　　　　皮相電流　Ｉｚ　は　５Ａ　となるから， 　　　　皮相電力は　１８０Ｖ×５Ａ＝９００ＶＡ 　　　　２辺が３および４のとき，斜辺５は，常識。 　　　　忘れたら　√（３２＋４２）＝√２５＝５ 初出：2017/02/12　 改版：2020/12/11
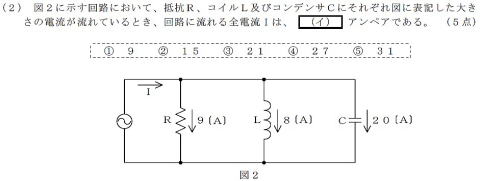
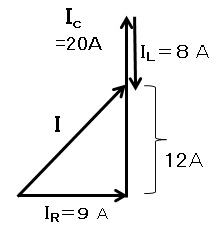
(f)	H25#1_問題2_(2)	【解き方】 　　　並列回路なので，各素子の端子電圧は等しい。 　　　そこで， 　　　電流ベクトル図で各素子の電流を表し 　　　電流Ｉを求める 　　　　 　　　 　　　　　Ｉ＝√（９×９＋１２×１２） 　　　　　＝√（８１＋144） 　　　　　＝√（225） 　　回答�@〜�Dを二乗して，２２５になるものを探す。 初出：2017/02/12　 改版：2020/12/11
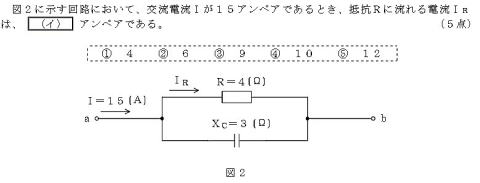
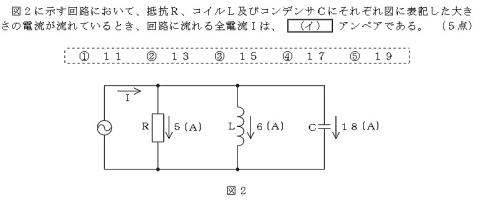
（ｆ’）	H29#2_問題２_(2)	【正攻法でない解き方？】 　　題意から， 　　電流ベクトル図を，絶対値で扱う方法 　　　　底辺（ＩＲ）が５（Ａ） 　　　　高さ（Ｉc）が１２（Ａ）　←　１８−６ 　　　　　　　　　　　 　　５，１２なのでいつもの３，４，５の比率使えず 　　　　　ので，がまんして計算 　　全電流Ｉ＝√（５×５＋１２×１２） 　　　　　　　＝√（25＋144） 　　　　　　　＝√169　　・・・・この値よく見かけますね 　　　　　　　＝13 初出：2017/02/12

※記載内容に不明点などあった際は，下記メールアドレスまで，おしらせいただければ幸いです。
junklaboz　@yahoo.co.jp　　←スペースはつめてください　

著作権情報
初版　　　　　: 2016/12/29
最終更新日 : 2020/12/10
.